循环神经网络 (Recurrent Neural Networks) 简称RNN广泛应用自然语言处理的中的语音识别,手书识别以及机器翻译等领域。
RNN概述
对于训练样本输入是连续的序列,且序列的长短不一,比如基于时间的序列:一段段连续的语音,一段段连续的手写文字。这些序列比较长,且长度不一,比较难直接的拆分成一个个独立的样本来通过DNN/CNN进行训练。
而对于这类问题,RNN则比较的擅长。RNN假设我们的样本是基于序列的。比如是从序列索引1到序列索引τ的。对于这其中的任意序列索引号\(t\),它对应的输入是对应的样本序列中的\(x^{(t)}\)。而模型在序列索引号t位置的隐藏状态\(h^{(t)}\),则由\(x^{(t)}\)和在\(t−1\)位置的隐藏状态\(h^{(t-1)}\)共同决定。在任意序列索引号\(t\),我们也有对应的模型预测输出\(o^{(t)}\)。通过预测输出\(o^{(t)}\)和训练序列真实输出\(y^{(t)}\),以及损失函数\(L^{(t)}\),我们就可以用DNN类似的方法来训练模型,接着用来预测测试序列中的一些位置的输出。
RNN模型
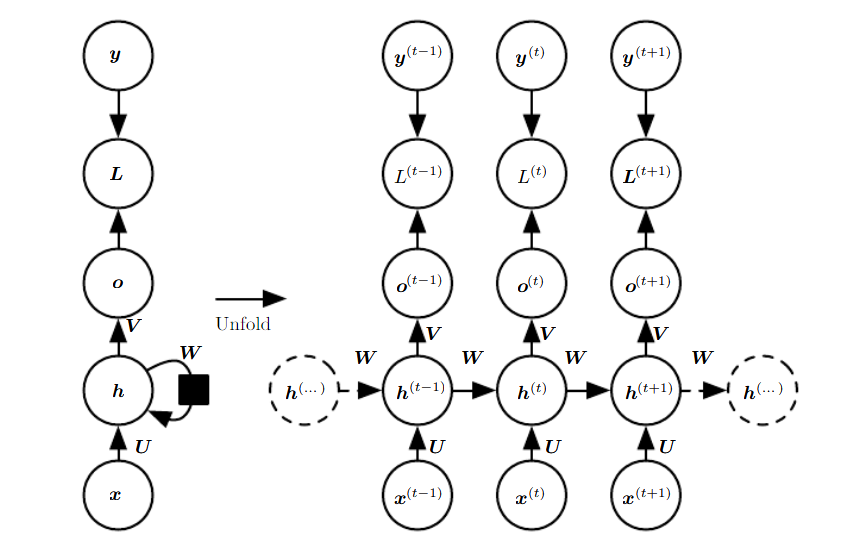
RNN模型示意图
如图所示为RNN模型示意图,该幅图描述了在序列索引号t附近RNN的模型。其中:
\(x^{(t)}\)代表在序列索引号tt时训练样本的输入。同样的,\(x^{(t-1)}\)和\(x^{(t+1)}\)代表在序列索引号\(t-1\)和\(t+1\)时训练样本的输入。
\(h^{(t)}\)代表在序列索引号\(t\)时模型的隐藏状态。\(h^{(t)}\)由\(x^{(t)}\)和\(h^{(t−1)}\)共同决定。
\(o^{(t)}\)代表在序列索引号\(t\)时模型的输出。\(o^{(t)}\)只由模型当前的隐藏状态\(h^{(t)}\)决定。
\(L^{(t)}\)代表在序列索引号\(t\)时模型的损失函数。
\(y^{(t)}\)代表在序列索引号tt时训练样本序列的真实输出。
\(U,V,W\)这三个矩阵是我们的模型的线性关系参数,它在整个RNN网络中是共享的,这点和DNN很不相同。 也正因为是共享了,它体现了RNN的模型的“循环反馈”的思想。
RNN向前传播算法
有了上面的模型,RNN的前向传播算法就很容易得到了。
对于任意一个序列索引号\(t\),我们隐藏状态\(h^{(t)}\)由\(x^{(t)}\)和\(h^{(t−1)}\)得到:
\[h^{(t)}=\sigma(Ux^{(t)}+Wh^{(t)}+b)\]
其中\(\sigma\)为RNN的激活函数,一般为\(tanh\),\(b\)为线性关系的偏倚。
序列索引号\(t\)时模型的输出\(o^{(t)}\)的表达式比较简单:
\[o^{(t)}=Vh^{(t)}+co^{(t)}=Vh^{(t)}+c\]
在最终在序列索引号tt时我们的预测输出为:
\[y^{(t)}=\sigma(o^{(t)})y^{(t)}=\sigma(o^{(t)})\]
通常由于RNN是识别类的分类模型,所以上面这个激活函数一般是softmax。
通过损失函数\(L^{(t)}\),比如对数似然损失函数,我们可以量化模型在当前位置的损失,即\(\hat y^{(t)}\)和\(y^{(t)}\)的差距。
RNN反向传播算法推导
为了简化描述,这里的损失函数我们为对数损失函数,输出的激活函数为softmax函数,隐藏层的激活函数为tanh函数。
对于RNN,由于我们在序列的每个位置都有损失函数,因此最终的损失\(L\)为:
\[L=\sum_{t=1}^\tau L^{(t)}\]
若激活函数为sigmoid,则f'(x)=f(x)(1-f(x))
若激活函数为tanh,则f'(x)=1-f(x)*f(x)接下来以依次计算梯度:
\[\frac{\partial L}{\partial c}=\sum_{t=1}^\tau \frac{\partial L^{(t)}}{\partial c}=\sum_{t=1}^\tau \frac{\partial L^{(t)}}{\partial o^{(o)}}\frac{\partial o^{(o)}}{\partial c}=\sum_{t=1}^\tau \hat y^{(t)}-y^{(t)}\]
\[\frac{\partial L}{\partial V}=\sum_{t=1}^\tau \frac{\partial L^{(t)}}{\partial V}=\sum_{t=1}^\tau \frac{\partial L^{(t)}}{\partial o^{(o)}}\frac{\partial o^{(o)}}{\partial V}=\sum_{t=1}^\tau (\hat y^{(t)}-y^{(t)})(h^{(t)})^T\]
对于\(W\)在某一序列位置\(t\)的梯度损失需要反向传播一步步的计算。我们定义序列索引\(t\)位置的隐藏状态的梯度为:
\[\delta^{(t)}=\frac{\partial L}{\partial h^{(t)}}\]
因此有:
\[\delta^{(t)}=\frac{\partial L}{\partial h^{(t)}}=V^T(\hat y^{(t)}-y^{(t)})\]
\[\frac{\partial L}{\partial W}=\sum_{t=1}^\tau \frac{\partial L}{\partial h^{(t)}}\frac{\partial h^{(t)}}{\partial W}=\sum_{t=1}^\tau diag(1-(h^{(t)})^2)\delta^{(t)}(h^{(t-1)})^T\]
\[\frac{\partial L}{\partial b}=\sum_{t=1}^\tau \frac{\partial L}{\partial h^{(t)}}\frac{\partial h^{(t)}}{\partial b}=\sum_{t=1}^\tau diag(1-(h^{(t)})^2)\delta^{(t)}\]
\[\frac{\partial L}{\partial U}=\sum_{t=1}^\tau \frac{\partial L}{\partial h^{(t)}}\frac{\partial h^{(t)}}{\partial U}=\sum_{t=1}^\tau diag(1-(h^{(t)})^2)\delta^{(t)}(x^{(t)})^T\]
参考文献
2.CS231n Convolutional Neural Networks for Visual Recognition, Stanford