长短期记忆 (Long Short Term Memeory)简称LSTM,可以避免常规RNN的梯度消失,因此在工业界得到了广泛的应用。
LSTM概述
LSTM传播如图所示:
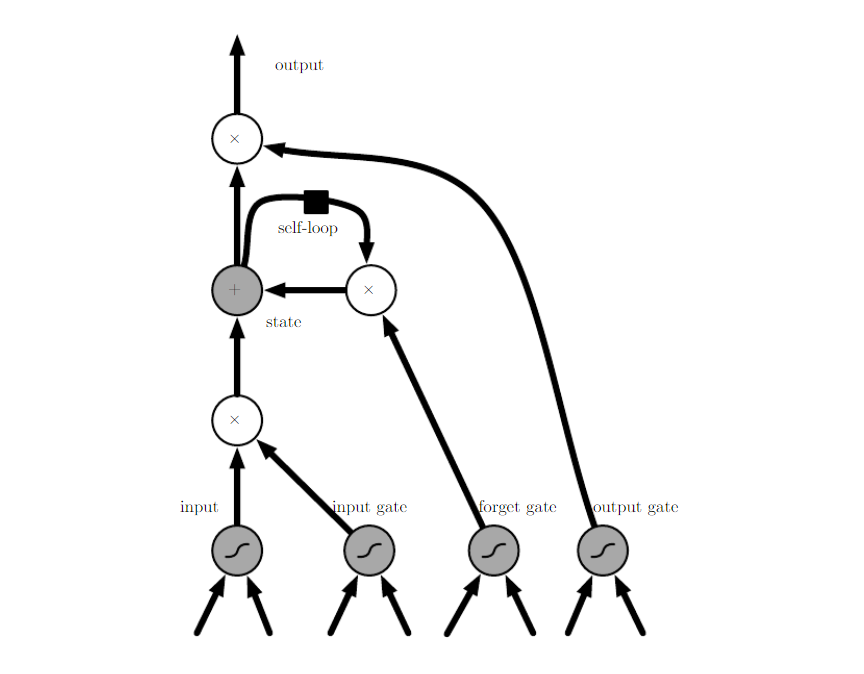
LSTM传播示意图
LSTM向前传播算法
LSTM模型有两个隐藏状态\(h^{(t)}\),\(C^{(t)}\),模型参数几乎是RNN的四倍,向前传播过程在每个序列索引位置的过程为:
- 更新遗忘门输出:
\[f^{(t)}=\sigma(W_fh^{(t-1)}+U_fs^{(t)}+b_f)\]
2)更新输入门两部分输出:
\[i^{(t)}=\sigma(W_ih^{(t-1)}+U_ix^{(t)}+b_i)\]
\[a^{(t)}=tant(W_ah^{(t-1)}+U_ax^{(t)}+b_a)\]
3)更新细胞状态:
\[C^{(t)}=C^{(t-1)}\odot f^{(t)}+i^{(t)}\odot a^{(t)}\]
- 更新输出门:
\[o^{(t)}=\sigma(W_oh^{(t-1)}+U_ox^{(t)}+b_o)\]
\[h^{(t)}=o^{(t)}\odot tant(C^{(t)})\]
- 更新当前序列索引预测输出:
\[\hat y^{(t)}=\sigma(Vh^{(t)}+c)\]
LSTM反向传播算法推导
首先我们定义两个\(\delta\),即:
\[\delta_h^{(t)}=\frac{\partial L}{\partial h^{(t)}}\]
\[\delta_C^{(t)}=\frac{\partial L}{\partial C^{(t)}}\]
但是在最后的序列索引位置\(\tau\)的\(\delta_h^{(\tau)}\)和\(\delta_C^{(\tau)}\)为:
\[\delta_h^{(\tau)}=\frac{\partial L}{\partial O^{(\tau)}}\frac{\partial O^{(\tau)}}{\partial h^{(\tau)}}=V^T(\hat y^{(\tau)}-y^{(\tau)})\]
\[\delta_C^{(\tau)}=\frac{\partial L}{\partial h^{(\tau)}}\frac{\partial h^{(\tau)}}{\partial C^{(\tau)}}=\delta_h^{(\tau)}\odot o^{(\tau)}\odot(1-tanh^2(C^{(\tau)}))\]
接着我们由\(\delta_C^{(t+1)}\)反向推导\(\delta_C{(t)}\)
\[\delta_h^{(t)}=\frac{\partial L}{\partial h^{(t}}=V^T(\hat y^{(t)}-y^{(t)})\]
\[\delta_C^{(t}=\frac{\partial L}{\partial C^{(t+1)}}\frac{\partial C^{(t+1)}}{\partial C^{(t)}}+\frac{\partial L}{\partial h^{(t)}}\frac{\partial h^{(t)}}{\partial C^{(t)}}=\delta_C^{(t+1)}\odot f^{(t+1)}+\delta_h^{(t)}\odot o^{(t)}\odot(1-tanh^2(C^{(t)}))\]
有了\(\delta_h^{(t)}\)以及\(\delta_C^{(t)}\)其他参数就很容易计算:
\[\frac{\partial L}{\partial W_f}=sum_{t=1}^\tau\frac{\partial L}{\partial C^{(t)}}\frac{\partial C^{(t)}}{\partial f^{(t)}}\frac{\partial f^{(t)}}{\partial W_f}=\sum){t=1}^\tau\delta_C^{(t)}\odot C^{(t-1)}\odot f^{(t)}(1-f^{(t)})(h^{(t-1)})^T\]
参考文献
2.CS231n Convolutional Neural Networks for Visual Recognition, Stanford